Understanding image sharpness part 1:
Introduction to resolution and MTF curves
by Norman Koren
 |
|
 A
photograph's detail is an integral part of its appeal. Many
photographers
spend a great deal of time, energy and money acquiring equipment to
make
sharp images. Back in the film era, if 35mm didn't satisfy them, they
invested in medium
format, 4x5,
8x10, or larger.
(I know two who use
8x20 inch
cameras.) The digital versus film debate is now mostly settled (2007),
but there is still some debate over the relationship between the number
of megapixels and image quality. I love sharpness and
detail,
but I take my camera gear on long hikes, so I prefer to carry
lightweight
equipment. I need to know what it can achieve, how to get the most out
of it and what I'm trading off by not going to a larger format, apart
from
saving my back. That's what motivated this study.
A
photograph's detail is an integral part of its appeal. Many
photographers
spend a great deal of time, energy and money acquiring equipment to
make
sharp images. Back in the film era, if 35mm didn't satisfy them, they
invested in medium
format, 4x5,
8x10, or larger.
(I know two who use
8x20 inch
cameras.) The digital versus film debate is now mostly settled (2007),
but there is still some debate over the relationship between the number
of megapixels and image quality. I love sharpness and
detail,
but I take my camera gear on long hikes, so I prefer to carry
lightweight
equipment. I need to know what it can achieve, how to get the most out
of it and what I'm trading off by not going to a larger format, apart
from
saving my back. That's what motivated this study.
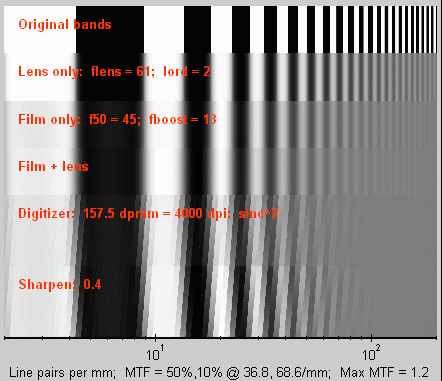
The sharpness of a photographic imaging system or of a component of the system (lens, film, image sensor, scanner, enlarging lens, etc.) is characterized by a parameter called Modulation Transfer Function (MTF), also known as spatial frequency response. We present a unique visual explanation of MTF and how it relates to image quality. A sample is shown on the right. The top is a target composed of bands of increasing spatial frequency, representing 2 to 200 line pairs per mm (lp/mm) on the image plane. Below you can see the cumulative effects of the lens, film, lens+film, scanner and sharpening algorithm, based on accurate computer models derived from published data. If this interests you, read on. It gets a little technical, but I try hard to keep it readable.
| The companion website,
Imatest.com,
describes a software tool you can use to measure MTF and other factors
that contribute to image quality in digital cameras and digitized film
images. |
| Green is for geeks. Do you get excited by a good equation? Were you passionate about your college math classes? Then you're probably a math geek— a member of a maligned and misunderstood but highly elite fellowship. The text in green is for you. If you're normal or mathematically challenged, you may skip these sections. You'll never know what you missed. |
| MTF
is the spatial frequency response of an imaging
system or a component;
it is the contrast at a given spatial frequency relative to low
frequencies. Spatial frequency is typically measured in cycles or line pairs per millimeter (lp/mm), which is analogous to cycles per second (Hertz) in audio systems. Lp/mm is most appropriate for film cameras, where formats are relatively fixed (i.e., 35mm full frame = 24x36mm), but cycles/pixel (c/p) or line widths per picture height (LW/PH) may be more appropriate for digital cameras, which have a wide variety of sensor sizes. High spatial frequencies correspond to fine image detail. The more extended the response, the finer the detail— the sharper the image. |
Most of
us are familiar with the frequency of sound, which is
perceived
as pitch and measured in cycles per second, now called Hertz. Audio
components—
amplifiers, loudspeakers, etc.— are characterized by frequency
response
curves.
MTF
is also
a frequency response, except that it involves spatial
frequency—
cycles (line pairs) per distance (millimeters or
inches) instead
of time. The mathematics is the same. The plots on
these pages have
spatial frequencies that increase continuously from left to right. High
spatial frequencies correspond to fine image detail. The response of
photographic
components (film, lenses, scanners, etc.) tends to roll off at high
spatial
frequencies. These components can be thought of as
lowpass filters— filters that pass low frequencies and
attenuate high
frequencies.
| Line
pairs or
lines?
All MTF charts and most resolution charts display spatial frequency in cycles or line pairs per unit length (mm or inch). But there are exceptions. An old standard for measuring TV resolution uses line widths instead of pairs, where there are two line widths per pair, over the total height of the display. When dpreview.com recommends multiplying the chart values in its lens tests by 100 to get the total vertical lines in the image, they refer to line widths, not pairs. Confusing, but I try to keep it straight. Imatest SFR displays MTF in cycles (line pairs) per pixel, line widths per picture height (LW/PH; derived from TV measurements), and line pairs per distance (mm or in). |
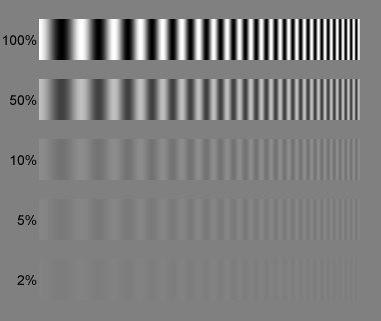 The
essential meaning of MTF is rather simple. Suppose you have a pattern
consisting
of a pure tone (a sine wave). At frequencies where the MTF of an
imaging
system or a component (film, lens, etc.) is 100%, the pattern is
unattenuated—
it retains full contrast. At the frequency where MTF is 50%, the
contrast
half its original value, and so on. MTF is usually
normalized to
100% at very low frequencies. But it can go above 100% with interesting
results.
The
essential meaning of MTF is rather simple. Suppose you have a pattern
consisting
of a pure tone (a sine wave). At frequencies where the MTF of an
imaging
system or a component (film, lens, etc.) is 100%, the pattern is
unattenuated—
it retains full contrast. At the frequency where MTF is 50%, the
contrast
half its original value, and so on. MTF is usually
normalized to
100% at very low frequencies. But it can go above 100% with interesting
results.
Contrast levels from 100% to 2% are illustrated on the right for a variable frequency sine pattern. Contrast is moderately attenuated for MTF = 50% and severely attenuated for MTF = 10%. The 2% pattern is visible only because viewing conditions are favorable: it is surrounded by neutral gray, it is noiseless (grainless), and the display contrast for CRTs and most LCD displays is relatively high. It could easily become invisible under less favorable conditions.
How is MTF related to lines per millimeter resolution? The old resolution measurement— distinguishable lp/mm— corresponds roughly to spatial frequencies where MTF is between 5% and 2% (0.05 to 0.02). This number varies with the observer, most of whom stretch it as far as they can. An MTF of 9% is implied in the definition of the Rayleigh diffraction limit.
Perceived image sharpness (as distinguished from traditional lp/mm resolution) is closely related to the spatial frequency where MTF is 50% (0.5)— where contrast has dropped by half.One important detail: MTF is not the same as grain. Grain increases with film speed: MTF is less sensitive to film speed.
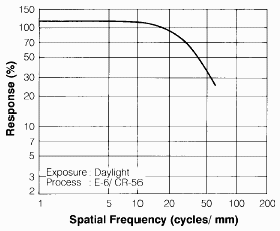
| The
MTF curve on the right is for Fuji's highly
regarded Provia 100F
slide film. It's typical except for one detail: MTF isn't 100%
at low spatial frequencies. This is an error— perhaps the
work of an overly
creative marketing department. The 50% MTF frequency ( f50
)
is about 42 lp/mm. MTF is only shown as far as 60 lp/mm. The resolution
of this film is rated as 60 lp/mm for 1.6:1 chart contrast and 140
lp/mm
for 1000:1 chart contrast. The latter number may be of interest to
astronomers,
but it has little to do with the perceived image sharpness of any
realistic
scenes.
The figure below represents a sine pattern (pure frequencies) with spatial frequencies from 2 to 200 cycles (line pairs) per mm on a 0.5 mm strip of film. The top half of the sine pattern has uniform contrast. The bottom half illustrates the effects of Provia 100F on the MTF. Pattern contrast drops to half at 42 cycles/mm. |
 |

| A
more precise definition of MTF based
on sine patterns: MTF is the contrast at a given spatial frequency ( f
) relative to contrast at low frequencies. These equations are used in
the page on
Lens
testing to calculate MTF from an image of a chart consisting
of sine
patterns of various frequencies, where the sine pattern contrast in the
original chart is assumed to be constant with frequency. (This series
uses
charts of continuously varying frequency.) Definitions:
.
MTF can also be defined as is the magnitude of the Fourier transform of the point or line spread function— the response of an imaging system to an infinitesimal point or line of light. This definition is technically accurate and equivalent to the sine pattern contrast definition, but can't be visualized as easily unless you're an engineer or physicist. |
|
Film imaging systems consist of a lens, film, developer,
scanner, image
editor, and printer (for digital prints) or lens, film, developer,
enlarging
lens, and paper (for traditional darkroom prints). Digital camera-based
imaging systems consist of a lens, digital image sensor, de-mosaicing
program,
image editor, and printer. Each of these components has a
characteristic
frequency response; MTF is merely its name in photography. The beauty
of
working in frequency domain is that
the
response of the entire system (or group of components) can be
calculated
by multiplying the responses of each component.
The
response of a component or system to a signal in time or space can be
calculated
by the following procedure.
|
| Resolution of an imaging system (old definition)— Using the assumption that resolution is a frequency where MTF is 10% or less, the resolution r of a system consisting of n components, each of which has an MTF curve similar to those shown below, can be approximated by the equation, 1/r = 1/r1 + 1/r2 + ... + 1/rn (equivalently, r = 1/(1/r1 + 1/r2 + ... + 1/rn )). This equation is adequate as a first order estimate, but not as accurate as multiplying MTF's. [I verified it with a bit of mathematics, assuming a second order MTF rolloff typical of the curves below. It's not sensitive to the MTF percentage that defines r. The approximation, 1/r2 = 1/r12 + 1/r22 + ..., is not accurate.] |
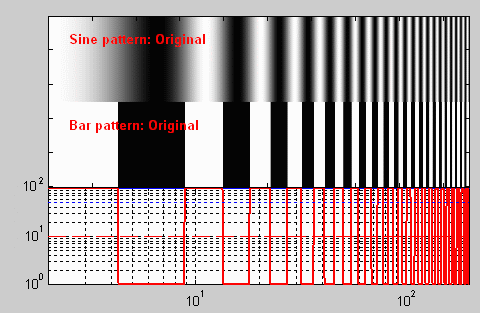
To visualize
the effects of MTF, we
have created a virtual target 0.5
mm in length, shown greatly enlarged on the right. The target consists
of a sine pattern and a bar pattern, both of which start at a low
spatial
frequency, 2 line pairs per millimeter (lp/mm) on the left, and
increase
logarithmically to 200 lp/mm on the right.
The mathematics for generating this function is rather tricky. It is discussed at the end of part 2.The red curve below the image represents the tonal densities (0 and 1) of the bar pattern. The vertical scale— 100 through 102— is for the MTF curves to come, not for the tonal density plot. |
 |
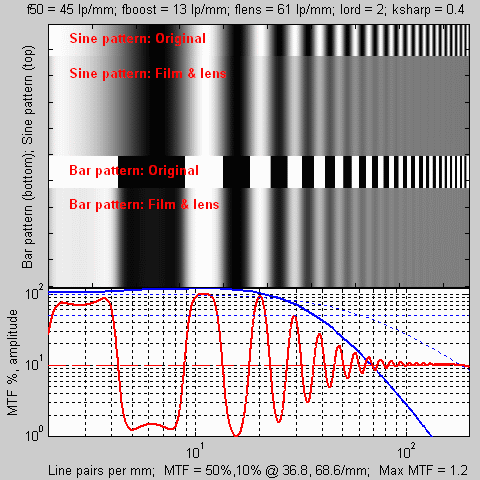 | The plot on the left illustrates the response of the virtual
target
to the combined effects of an excellent lens (a simulation of the
highly-regarded
Canon
28-70mm f/2.8L) and film (a simulation of Velvia). Both the
sine and
bar patterns (original and response) are shown. You'll find these plots
throughout this series as we simulate lenses, film, scanners,
sharpening,
and finally, digital cameras.
The red curve is the spatial response of the bar pattern to the film + lens. The blue curve is the combined MTF, i.e., the spatial frequency response of the film + lens, expressed in percentage of low frequency response, indicated on the scale on the left. (It goes over 100% (102).) The thin blue dashed curve is the MTF of the lens only. The edges in the bar pattern have been broadened, and there are small peaks on either side of the edges. The shape of the edge is inversely related to the MTF response: the more extended the MTF response, the sharper (or narrower) the edge. The mid-frequency boost of the MTF response is related to the small peaks on either side of the edges. |
| The leftmost edge in the plot is a portion
of
the
step response of the system (film + lens). A much
lower spatial
frequency is required to represent it properly. The impulse
response— the
response of the system to a narrow line (or impulse) is
also of interest. The impulse response is the derivative
of the
step response (d(step response)/dx). The MTF curve is related to the impulse response by a mathematical operation known as the Fourier transform ( F ), which is well-known to engineers and physicists. MTF response = F(impulse response) impulse response = F-1(MTF response) F-1 is the inverse Fourier transform. We'll spare the gentle reader from further equations— the topic is quite understandable without them. |
The image above represents only 0.5 mm of film, but takes up around 5 inches (13 cm) on my monitor. At this magnification (260x), a full frame 35mm image (24x36mm) would be 240 inches (6.2 meters) high and 360 inches (9.2 meters) wide. A bit excessive, but if you stand back from the screen you'll get an feeling for the effects of the lens, film, scanner (or digital camera), and sharpening on real images.
| The companion website, Imatest.com, describes a software tool you can use to measure MTF and other factors that contribute to image quality in digital cameras and digitized film images. |
 At
a distance d from the eye (which has a nominal
focal length of 16.5
mm), this corresponds to objects of length = (angle in radians)*d
= 0.000291*d. For
example, for an object viewed at a distance of
25 cm (about 10 inches), the distance you might use for close scrutiny
of an 8x10 inch
photographic print,
this would correspond to 0.0727 mm = 0.0029 inches. Since a line pair
corresponds
to two lines of this size, the corresponding spatial frequency is 6.88
lp/mm or 175 lp/inch. Assume now that the image was printed from a 35mm
frame enlarged 8x.
The corresponding
spatial frequency on the film would be 55 lp/mm.
At
a distance d from the eye (which has a nominal
focal length of 16.5
mm), this corresponds to objects of length = (angle in radians)*d
= 0.000291*d. For
example, for an object viewed at a distance of
25 cm (about 10 inches), the distance you might use for close scrutiny
of an 8x10 inch
photographic print,
this would correspond to 0.0727 mm = 0.0029 inches. Since a line pair
corresponds
to two lines of this size, the corresponding spatial frequency is 6.88
lp/mm or 175 lp/inch. Assume now that the image was printed from a 35mm
frame enlarged 8x.
The corresponding
spatial frequency on the film would be 55 lp/mm.
This means that for an 8x10 inch print, the MTF of a 35mm camera (lens + film, etc.) above 55 lp/mm, or the MTF of a digital camera above 2800 LW/PH (Line Widths per Picture Height) measured by Imatest SFR, has no effect on the appearance of the print. That's why the highest spatial frequencies used in manufacturer's MTF charts is typically 40 lp/mm, which provides an excellent indication of a lens's perceived sharpness in an 8x10 inch print enlarged 8x. Of course higher spatial frequencies are of interest for larger prints.
Standard Depth of Field (DOF) scales on lenses are based on the assumption, made in the 1930s, that the smallest feature of importance, viewed at 25 cm, is 0.01 inches— 3 times larger. It shouldn't be a surprise that focus isn't terribly sharp at the DOF limits. See the DOF page for more details.
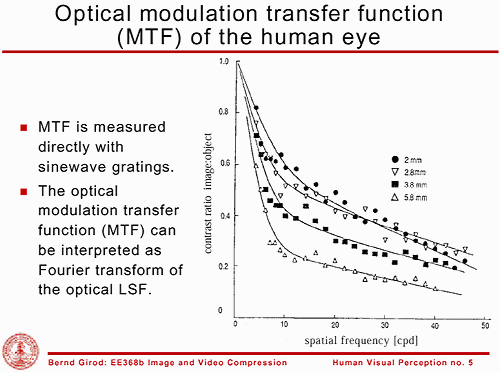
The statement that the eye cannot distinguish features smaller than one minute of an arc is, of course, oversimplified. The eye has an MTF response, just like any other optical component. It is illustrated on the right from the Handout #9: Human Visual Perception from Stanford University course EE368B - Image and Video Compression by Professor Bernd Girod. The horizontal axis is angular frequency in cycles per degree (CPD). MTF is shown for pupil sizes from 2 mm (bright lighting; f/8), to 5.8 mm (dim lighting; f/2.8). At 30 CPD, corresponding to a one minute of an arc feature size, MTF drops from 0.4 for the 2 mm pupil to 0.16 for the 5.8 mm pupil. (Now you know your eye's f-stop range. It's similar to compact digital cameras.) Another Stanford page has Matlab computer models of the eye's MTF.
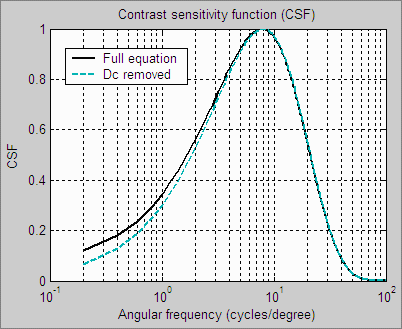 | The
human eye's MTF, which is limited at
high angular frequencies by the
eye's optical system and cone density, does not tell the whole story of
the eye's response. Neuronal interactions such
as lateral inhibition
limit the eye's response at low
angular frequencies, i.e., the eye is insensitive to very gradual
changes in density. The eye's overall response is called its contrast
sensitivity function (CSF). Various
studies place
the peak CSF for bright light levels (typical of print viewing
conditions) between 6 and 8 cycles per degree. The graph on the left
uses an approximation (equations below) that peaks just below 8
cycles/degree. CSF is used in measures of perceptual image sharpness called Acutance and Subjective Quality Factor (SQF), which includes MTF, CSF, print size, and typical viewing distance. SQF has been used since the 1970s inside Kodak and Polaroid, but it was difficult to calculate, and hence remained obscure, until it was incorporated into Imatest in 2006. |
The following formula for CSF is
relatively simple, recent, and
fits the data well. The source is J. L. Mannos, D. J.
Sakrison, ``The Effects of a Visual Fidelity Criterion on the Encoding
of Images'', IEEE Transactions on Information Theory, pp. 525-535, Vol.
20, No 4, (1974), cited on this page of Kresimir Matkovic's 1998 PhD
thesis.CSF( f ) = 2.6 (0.0192 + 0.114 f ) exp(-0.114 f )1.1The 2.6 multiplier can be removed and the equation can be simplified somewhat. The dc term (0.0192) can be dropped with very little effect. CSF( f ) = (0.0192 + 0.114 f ) exp(-0.1254 f ) |
Additional
explanations of human visual
acuity can be found on pages
from the Nondestructive
testing resource center and Stanford
University. Page 3 from Stanford has a plot of the MTF of the
human
eye. I believe the x-axis units (CPD) are Cycles per Degree, where a
pair
of 1/60 degree features corresponds to 30 CPD.

| Images and text copyright © 2000-2013 by Norman Koren. Norman Koren lives in Boulder, Colorado, where he worked in developing magnetic recording technology for high capacity data storage systems until 2001. Since 2003 most of his time has been devoted to the development of Imatest. He has been involved with photography since 1964. |  |